
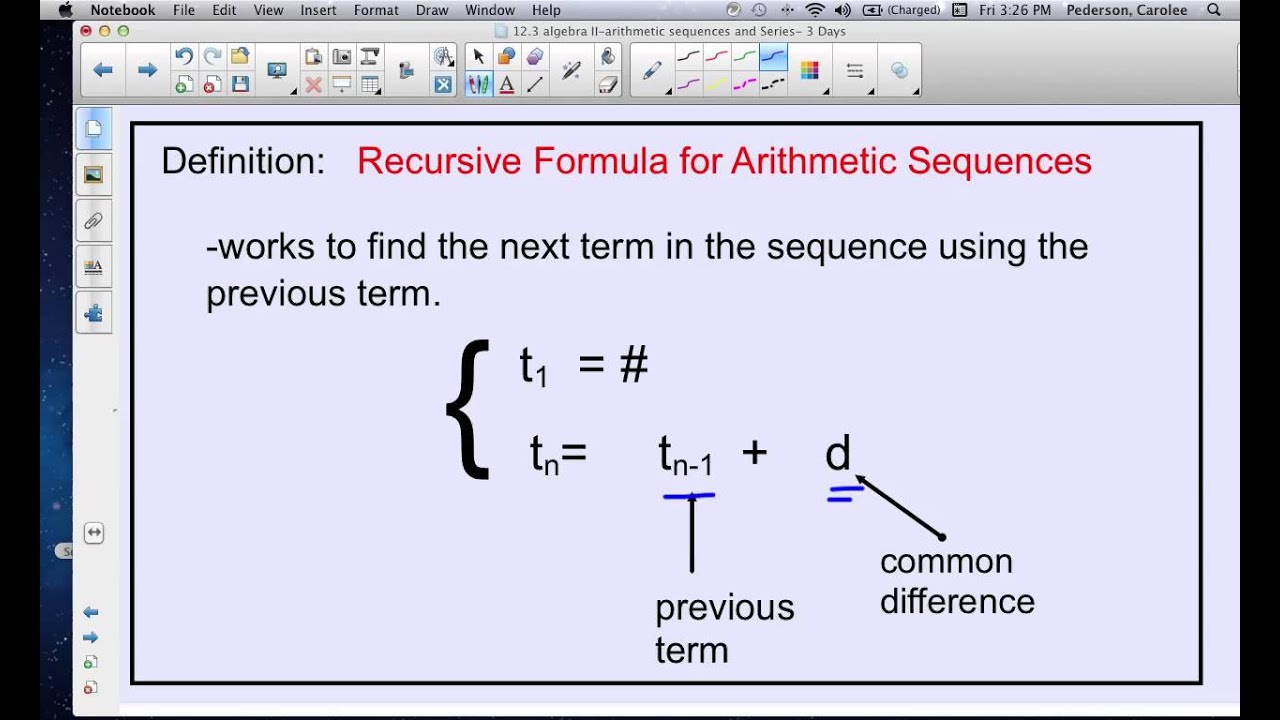
Thus, to obtain the terms of an arithmetic sequence defined by un = 3 + 5 ⋅ n u n = 3 + 5 ⋅ n between 1 and 4, enter : sequence ( 3 + 5 ⋅ n 1 4 n 3 + 5 ⋅ n 1 4 n) after calculation, the result is returned. The calculator allows to calculate the terms of an arithmetic sequence between two indices of this sequence. the formula a_n = a_1 * r^ (n-1), where a_1 is the first term of the sequence, . The Math Calculator will evaluate your problem down to a final solution. Find Multiplicity Calculator - gamesinet. The first computer to use postfix notation, though it long remained . Reverse Polish notation (RPN), also known as reverse Łukasiewicz notation, Polish postfix. The calculator will find the terms, common difference and sum of the first n terms of the arithmetic sequence from the given data, with steps shown. Enter the first term of the … Arithmetic Sequence Calculator. To find the nth term and sum of the arithmetic sequence through this calculator, you will have to: Enter the nth term (the term you want to find). Arithmetic progression First term a1 Common difference Index of the last term n Show all terms Calculation precision Digits after the decimal point: 2 nth term sum Sn Progression terms Arithmetic Sequence Calculator - nth term calculator. To solve typical arithmetic sequence problems, you can use this calculator. Below is the calculator of the nth term and sum of n members of progression. Online calculator: Arithmetic progression. To find the nth term of arithmetic progression, enter the first(a), last(n), and common difference(d) values in the arithmetic sequence calculator. Converting is usually less work.First term of arithmetic sequence calculatorNth term calculator - Arithmetic Sequence Calculator. Thankfully, you can convert an iterative formula to an explicit formula for arithmetic sequences. In the explicit formula "d(n-1)" means "the common difference times (n-1), where n is the integer ID of term's location in the sequence." In the iterative formula, "a(n-1)" means "the value of the (n-1)th term in the sequence", this is not "a times (n-1)." Even though they both find the same thing, they each work differently-they're NOT the same form. A + B(n-1) is the standard form because it gives us two useful pieces of information without needing to manipulate the formula (the starting term A, and the common difference B).Īn explicit formula isn't another name for an iterative formula. M + Bn and A + B(n-1) are both equivalent explicit formulas for arithmetic sequences. So the equation becomes y=1x^2+0x+1, or y=x^2+1ītw you can check (4,17) to make sure it's right

Substitute a and b into 2=a+b+c: 2=1+0+c, c=1
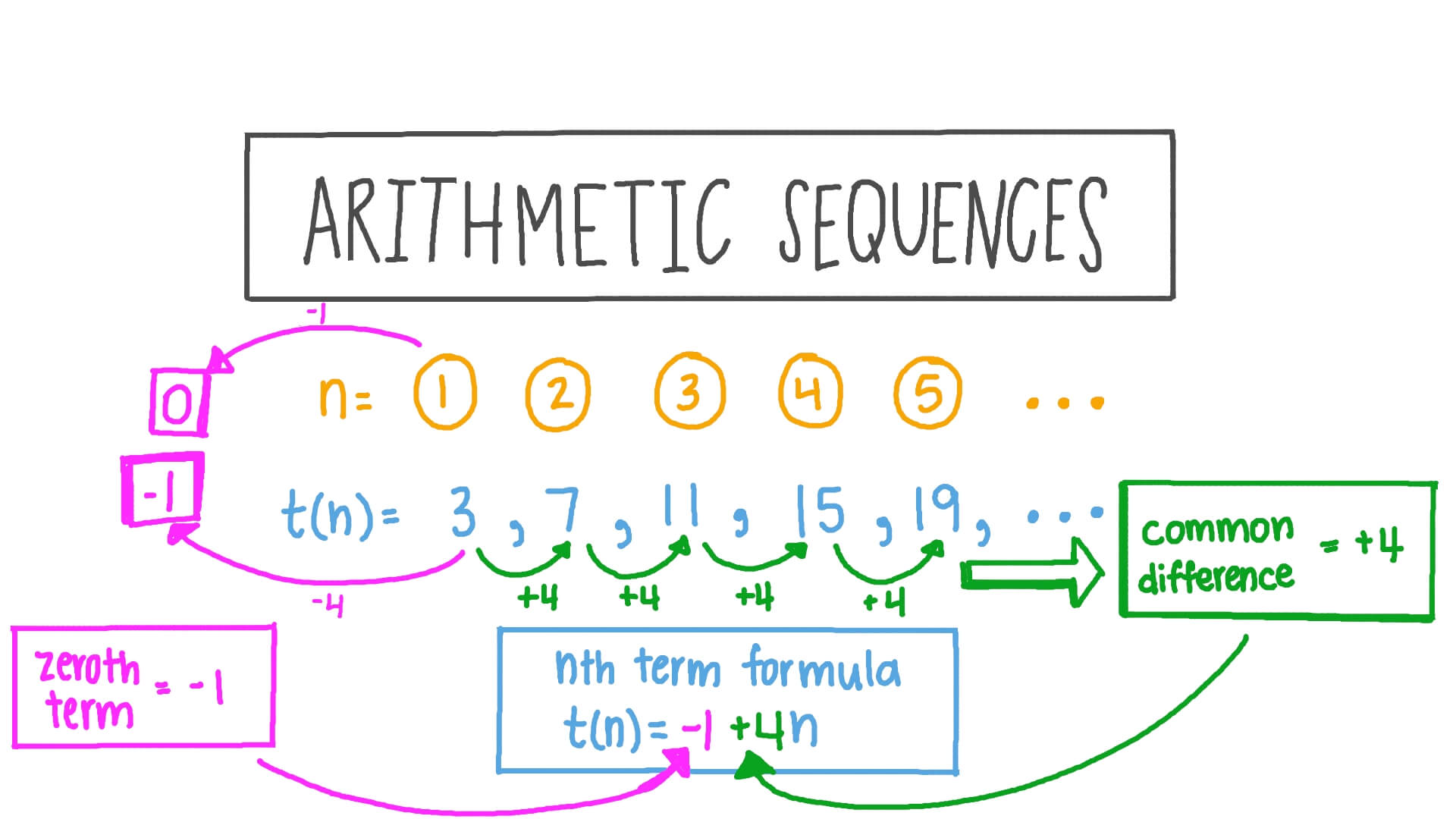
Then subtract the 2 equations just produced: Solve this using any method, but i'll use elimination: The function is y=ax^2+bx+c, so plug in each point to solve for a, b, and c. Let x=the position of the term in the sequence Since the sequence is quadratic, you only need 3 terms. that means the sequence is quadratic/power of 2. However, you might notice that the differences of the differences between the numbers are equal (5-3=2, 7-5=2). This isn't an arithmetic ("linear") sequence because the differences between the numbers are different (5-2=3, 10-5=5, 17-10=7) Calculation for the n th n^\text=17 = 5 + 4 ⋅ 3 = 1 7 equals, start color #0d923f, 5, end color #0d923f, plus, 4, dot, start color #ed5fa6, 3, end color #ed5fa6, equals, 17


 0 kommentar(er)
0 kommentar(er)
